Vous vous êtes peut-être déjà demandé comment calculer la focale d’un objectif ou comment déterminer le zoom d’un appareil photo. La focale est une notion clé en optique, qui permet de mesurer la distance entre l’objectif et le point focal. Mais comment la calculer ? Comment trouver la distance focale formule ? Dans cet article, nous allons vous expliquer les différentes méthodes pour déterminer la focale d’un objectif, ainsi que la formule pour calculer la distance focale. Que vous soyez un photographe amateur ou professionnel, ces astuces vous seront utiles pour comprendre le fonctionnement de votre équipement et améliorer vos prises de vue.
Comment calculer la focale d’un objectif ?
Le calcul de la focale d’un objectif peut sembler complexe à première vue, mais il peut être facilement effectué en utilisant la formule appropriée. La formule la plus couramment utilisée pour calculer la focale d’un objectif est la formule de conjugaison, qui prend en compte la distance entre l’objet et l’objectif, la distance entre l’objectif et l’image, ainsi que la distance focale elle-même. Cette formule est représentée par l’équation suivante : D = f/g +2f +fg.
Cependant, il est important de noter que le résultat obtenu à partir de cette formule ne donne généralement pas une valeur entière ou une valeur de focale standardisée. Par conséquent, il est recommandé de recalculer la distance focale en fonction de la valeur standardisée la plus proche pour faciliter la compréhension et l’utilisation ultérieure de l’objectif.
En utilisant cette méthode de calcul, vous serez en mesure de déterminer la distance focale d’un objectif avec précision, ce qui vous permettra de sélectionner l’objectif parfait pour votre appareil photo et de capturer des images de qualité supérieure.
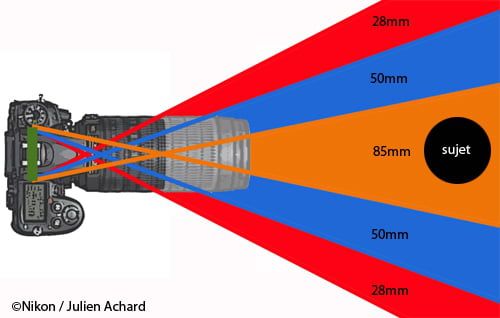
Découvrez aussi Quel objectif pour zoomer loin ?
Comment trouver F en optique ?
Pour trouver la distance focale en optique, il est important de comprendre que cela dépend de la vergence de l’objectif. La vergence est la capacité d’un objectif à focaliser la lumière. Plus la vergence est élevée, plus la distance focale sera courte.
La formule à utiliser pour calculer la distance focale est f’=dfrac{1}{C}. Cette formule nous permet de déterminer la distance focale en fonction de la vergence de l’objectif. La vergence est mesurée en dioptries (D) et représente l’inverse de la distance focale exprimée en mètres. Ainsi, plus la vergence est élevée, plus la distance focale est courte.
Il est important de noter que la distance focale est également influencée par la courbure de la lentille et l’indice de réfraction du matériau dont elle est faite. En général, les lentilles plus courtes sont plus convexes et ont un indice de réfraction plus élevé.
En fin de compte, pour trouver la distance focale en optique, il est nécessaire de connaître la vergence de l’objectif et d’appliquer la formule f’=dfrac{1}{C}. Cela permettra de déterminer la distance focale de l’objectif et de comprendre comment il focalise la lumière.
Comment déterminer le zoom d’un objectif ?
Pour déterminer le zoom d’un objectif, il est important de comprendre le concept de grossissement. Comme mentionné précédemment, le grosissement mesure la distance focale d’un objectif par rapport à un objectif de référence, qui est généralement le 50mm sur capteur 24×36.
Supposons que vous avez un objectif de 200mm pour 24×36. Le grossissement de cet objectif serait de 200/50 = 4, ce qui signifie qu’il a un grossissement de x4 par rapport à l’objectif de référence.
Le zoom d’un objectif est simplement la plage de focales qu’il peut couvrir. Par exemple, un objectif de 24-70mm a un zoom de 2,9x car la plage focale couverte est de 46mm (70-24). De même, un objectif de 70-200mm a un zoom de 2,8x car la plage focale couverte est de 130mm (200-70).
Il est important de noter que le grossissement et le zoom ne sont pas la même chose. Le grossissement mesure la distance focale d’un objectif par rapport à un objectif de référence, tandis que le zoom mesure la plage focale d’un objectif.
En conclusion, pour déterminer le zoom d’un objectif, il est important de connaître la plage focale qu’il couvre. Le grossissement, quant à lui, est utilisé pour comparer la distance focale d’un objectif par rapport à un objectif de référence.
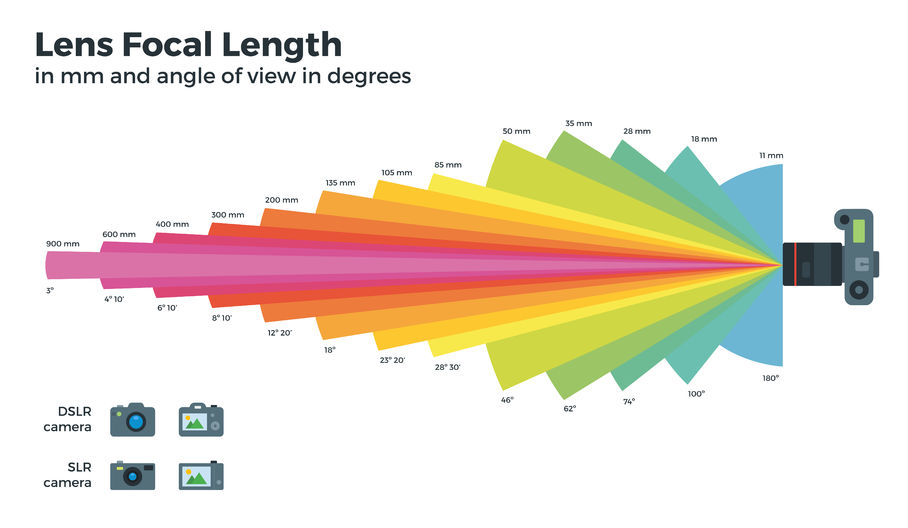
Comment donner la distance focale ?
La distance focale d’un objectif est un élément clé en optique, permettant notamment de déterminer la netteté d’une image. Pour trouver cette distance, il est possible de se référer à la relation de conjugaison de Descartes. Cette formule implique la connaissance de plusieurs paramètres, dont la position de l’objet et de l’image par rapport à l’objectif.
En reprenant la relation de conjugaison de Descartes, on peut trouver la distance focale en utilisant des positions spécifiques de l’objet et de l’image. En effet, si l’on cherche à avoir OA’ = -OA, cela revient à avoir OA = -2f’ et OA’ = 2f’. On peut alors utiliser ces valeurs pour résoudre la formule 1/OA’ – 1/OA = 1/OF’, et ainsi déterminer la distance focale de l’objectif.
Il est important de noter que cette méthode nécessite la connaissance précise des positions de l’objet et de l’image, ainsi que d’autres paramètres tels que la distance entre l’objet et l’objectif. Cependant, une fois ces données acquises, cette formule permet de calculer rapidement et efficacement la distance focale de l’objectif, permettant ainsi de réaliser des images nettes et précises.
>> Plus d’astuces Quel objectif pour un débutant ?
Comment on calcule l’image de F ?
Lorsqu’on parle du calcul de l’image de F, on se réfère à la fonction f(x) où F est la valeur de x qu’on souhaite évaluer. Pour effectuer ce calcul, il suffit de remplacer la variable x par la valeur de F dans la fonction f(x). En d’autres termes, on remplace x par F pour obtenir f(F).
Par exemple, si la fonction f(x) = 2x + 3 et que l’on souhaite calculer l’image de F = 4, il suffit de remplacer x par 4 dans la fonction f(x). Ainsi, on a f(4) = 2(4) + 3 = 11. La valeur de l’image de F est donc égale à 11.
Ce calcul est simple et peut être appliqué à toutes les fonctions mathématiques, y compris en optique. En effet, pour déterminer la position de l’image d’un objet à travers une lentille, il suffit d’appliquer les formules de l’optique géométrique. En utilisant la distance focale et les positions de l’objet et de l’image, il est possible de calculer la position de l’image de F pour une lentille donnée.
Il est donc important de comprendre le calcul de l’image de F pour pouvoir appliquer les concepts de l’optique géométrique et ainsi résoudre des problèmes complexes en optique.
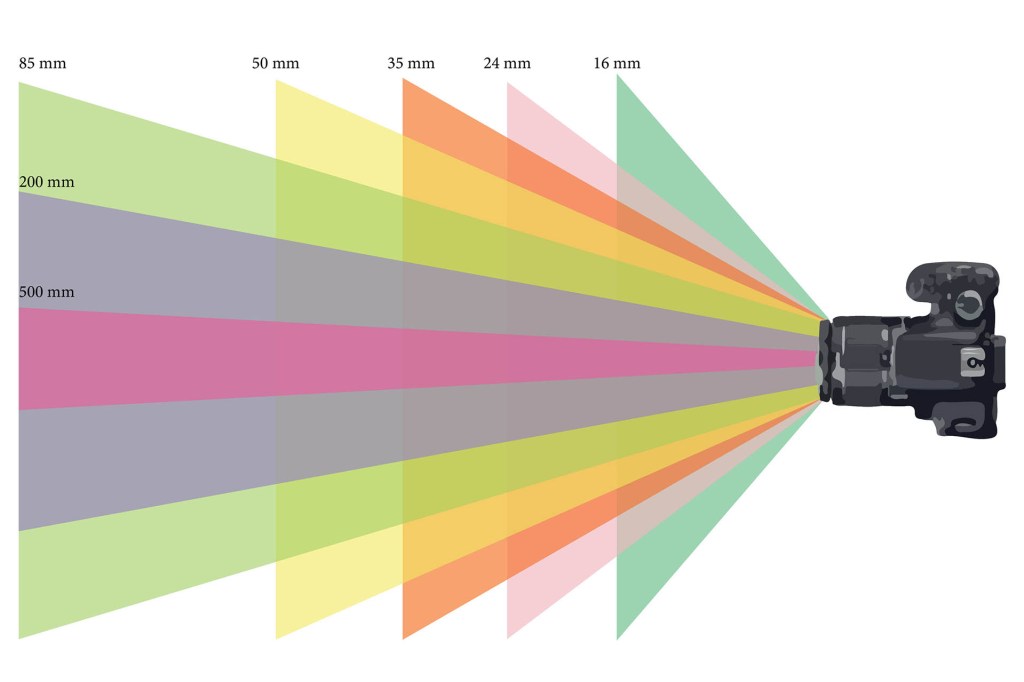
Comment déterminer F et F ?
Pour déterminer F et F, il est important de comprendre la signification de la notation utilisée. F et F sont respectivement les distances focales de l’objectif utilisé. La distance focale est la distance entre l’objectif et le point focal, c’est-à-dire le point où la lumière converge.
Pour trouver F et F, il est nécessaire de connaître le coefficient directeur de la tangente à C f au point d’abscisse a. Le coefficient directeur est représenté par f'(a) et peut être trouvé en utilisant la formule suivante :
f'(a) = (yB – yA) / (xB – xA)
Une fois que vous avez trouvé la valeur de f'(a), vous pouvez déterminer F et F en utilisant les formules suivantes :
F = 1 / f'(a)
F’ = 1 / (f'(a) – 1/F)
Il est important de noter que ces formules ne sont valables que pour les objectifs minces. Pour les objectifs épais, une formule différente doit être utilisée pour déterminer F et F’. En utilisant ces formules, vous pouvez facilement déterminer la distance focale de votre objectif et ajuster en conséquence la mise au point de votre appareil photo pour capturer des images nettes et claires.
Comment trouver la distance focale formule ?
La distance focale est une mesure importante en optique, car elle détermine la manière dont la lumière est focalisée sur l’objet à photographier. Pour trouver la distance focale d’un objectif, il existe une formule simple : f = Y'(L/Y). Cette formule prend en compte différents paramètres tels que la taille de l’image Y’, la taille de l’objet Y, et la distance entre l’objectif et l’objet L.
Il est important de noter que cette formule s’applique dans des conditions de vue éloignée, lorsque le grandissement optique est inférieur à 0,1. Le grandissement optique est une mesure qui permet de déterminer la taille de l’image par rapport à la taille de l’objet.
En utilisant cette formule, il est possible de calculer la distance focale d’un objectif avec précision. Il est également important de comprendre que la distance focale a une incidence directe sur le champ de vision de l’objectif. Plus la distance focale est grande, plus le champ de vision est étroit, et inversement.
En conclusion, la formule f = Y'(L/Y) est un outil utile pour déterminer la distance focale d’un objectif en optique. Elle prend en compte différents paramètres tels que la taille de l’image, la taille de l’objet et la distance entre l’objectif et l’objet. Il est important de comprendre l’impact de la distance focale sur le champ de vision de l’objectif, afin de choisir l’objectif le plus adapté à votre projet photographique.
Aller plus loin











Leave a Reply