Vous êtes à la recherche d’une méthode simple et efficace pour résoudre des problèmes de proportionnalité? Vous êtes au bon endroit! Dans cet article, nous allons vous expliquer en détail comment faire un produit en croix et répondre à toutes vos questions : quelle est la formule du produit en croix ? Quand apprend-on cette méthode ? Comment utiliser une règle de 3 pour trouver un pourcentage ? Comment faire un produit en croix avec des fractions ? Et enfin, comment faire un produit en croix pour résoudre le théorème de Thalès ? Vous allez découvrir toutes les astuces pour maîtriser cette méthode mathématique incontournable. Alors, prenez votre calculatrice et suivez le guide !
Comment faire 1 produit en croix ?
Le produit en croix est une méthode mathématique qui permet de trouver une quatrième grandeur proportionnelle à trois autres grandeurs données. Cette méthode est souvent utilisée dans les situations où l’on doit résoudre des problèmes de proportionnalité.
Pour réaliser un produit en croix, il faut suivre quelques étapes simples. Tout d’abord, il faut multiplier les deux informations connues en diagonale. Ensuite, il faut diviser le tout par la troisième information connue. Enfin, il suffit d’appliquer la formule suivante : x = c x b / a.
Il est important de noter que le produit en croix peut être utilisé dans différentes situations. Par exemple, il peut être utilisé pour trouver une quantité inconnue dans une recette de cuisine en utilisant les proportions des ingrédients. Il peut également être utilisé pour calculer le prix d’un produit en fonction de son poids et de son prix au kilo.
Le produit en croix est une méthode simple et efficace pour résoudre des problèmes de proportionnalité. Il est donc important de maîtriser cette méthode pour résoudre les problèmes mathématiques liés à la proportionnalité.

Découvrez aussi Comment faire de belles photos pour vendre ?
Quelle est la formule du produit en croix ?
Le produit en croix est une méthode de calcul mathématique qui permet de trouver une quatrième proportionnelle à trois autres valeurs connues. La formule du produit en croix est d=(b×c)÷a=b×ca, où d représente la valeur inconnue recherchée, b et c sont les deux premières valeurs connues, et a est la troisième valeur connue.
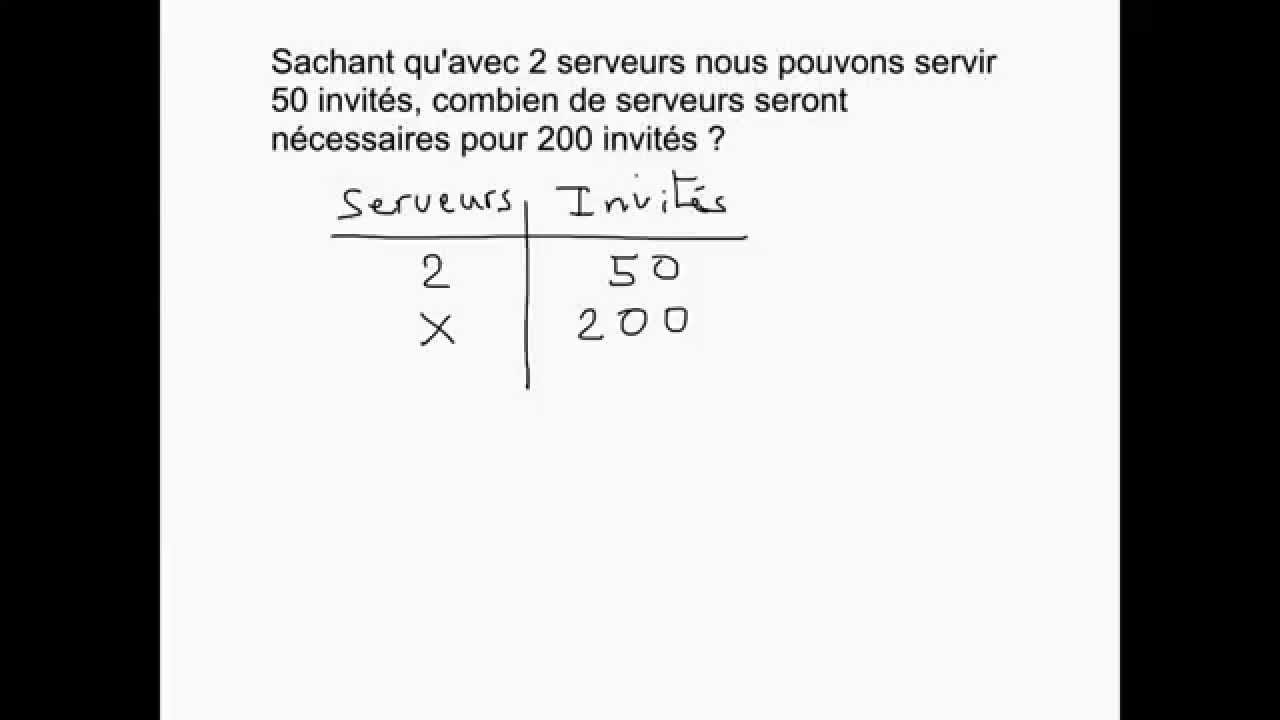
Pour utiliser cette formule, il suffit d’entrer les trois valeurs connues dans l’équation et de résoudre pour trouver la valeur inconnue. Par exemple, si vous connaissez que 2 pommes coûtent 3 euros, combien coûtent 5 pommes ?
En utilisant la formule du produit en croix, vous pouvez écrire :
d = (b × c) ÷ a = (2 × 5) ÷ 3 = 10 ÷ 3 = 3,33 euros
Ainsi, vous pouvez déduire que 5 pommes coûtent 3,33 euros.
Il est important de noter que le produit en croix est souvent utilisé dans les problèmes de proportionnalité, notamment dans les situations impliquant des pourcentages et des fractions. En prenant le temps de lire les exemples ci-dessous, vous pouvez avoir une idée plus précise de l’utilisation de cette méthode de calcul mathématique.
Quand Apprend-on le produit en croix ?
Le produit en croix est une méthode mathématique qui permet de résoudre des problèmes de proportionnalité. Cette méthode est enseignée en classe de quatrième, et elle peut être utilisée pour résoudre divers types de problèmes. Elle est très utile en mathématiques, mais aussi dans d’autres domaines tels que l’économie, le commerce, la science, etc.
Le produit en croix est une méthode simple et efficace qui peut être utilisée pour résoudre des problèmes de proportionnalité directe ou inverse. Cette méthode est souvent utilisée pour calculer des pourcentages, des taux de change, des distances, des vitesses, etc. Elle consiste à multiplier les termes en croix pour trouver une valeur inconnue.
En classe de quatrième, les élèves apprennent à utiliser cette méthode pour résoudre des problèmes de proportionnalité. Ils apprennent également à faire des règles de trois simples ou inverses pour résoudre des problèmes de pourcentage. Cette méthode est très importante pour les élèves, car elle leur permet de comprendre les concepts de proportionnalité et de pourcentage.
En conclusion, le produit en croix est une méthode mathématique essentielle pour résoudre des problèmes de proportionnalité. Elle est enseignée en classe de quatrième, et elle peut être utilisée dans de nombreux domaines. Les élèves doivent donc être attentifs lors de son apprentissage afin de maîtriser cette méthode et de l’utiliser efficacement dans leurs futurs travaux.

Comment faire une règle de 3 pour trouver un pourcentage ?
La règle de trois est une méthode mathématique très utile pour résoudre des problèmes de proportionnalité. Elle permet de trouver une valeur inconnue à partir de trois autres valeurs connues. Lorsque l’on doit trouver un pourcentage, la règle de trois est particulièrement efficace. Il suffit de suivre quelques étapes simples pour arriver à la réponse.
Tout d’abord, il faut déterminer la valeur initiale et le pourcentage. Ensuite, il faut multiplier la valeur initiale par le taux du pourcentage, puis diviser le résultat par 100. Cette opération permet d’obtenir la valeur partielle correspondant au pourcentage demandé. Pour faciliter les calculs, il est possible d’utiliser une calculatrice ou un tableur.
Par exemple, si vous voulez trouver le montant de la TVA sur un article dont le prix HT est de 100 euros et dont le taux de TVA est de 20%, vous pouvez utiliser la règle de trois. La valeur initiale est de 100 euros, le pourcentage est de 20%. En multipliant 100 par 20, puis en divisant par 100, on obtient une valeur partielle de 20 euros. Le montant de la TVA est donc de 20 euros.
En résumé, la règle de trois est une méthode simple et efficace pour trouver un pourcentage. En multipliant la valeur initiale par le pourcentage, puis en divisant par 100, on obtient la valeur partielle correspondante. Cette méthode peut être utilisée dans de nombreux domaines, comme la finance, le commerce ou les statistiques.
>> Plus d’astuces Comment faire un joli Pêle-mêle de photos ?
Comment faire un produit en croix avec des fraction ?
Le produit en croix est une méthode mathématique très utile pour trouver une valeur inconnue dans une proportion. Lorsque cette méthode est appliquée à des fractions, elle peut sembler un peu plus compliquée, mais elle reste tout aussi efficace. Pour utiliser le produit en croix avec des fractions, il est important de comprendre comment cela fonctionne.
Imaginons que nous avons deux fractions, a/b et c/d, et que nous voulons trouver la valeur de x dans la proportion a/b = x/c. Pour cela, nous devons utiliser le produit en croix, en multipliant le numérateur de la première fraction avec le dénominateur de la deuxième fraction et en multipliant le numérateur de la deuxième fraction avec le dénominateur de la première fraction. Nous obtenons alors l’équation ad = bc.
Pour illustrer cela, prenons l’exemple de 3/4 et x/6. Si nous voulons savoir quelle est la valeur de x pour que ces deux fractions soient proportionnelles, nous devons appliquer le produit en croix. Nous multiplions alors 3 par 6, ce qui donne 18, et nous multiplions 4 par x, ce qui donne 4x. Nous avons donc l’équation 3x = 24, et en résolvant pour x, nous trouvons que x = 8. Ainsi, la proportion 3/4 = 8/6 est vérifiée.
Il est important de noter que pour utiliser le produit en croix avec des fractions, les dénominateurs ne doivent pas être nuls. Si l’un des dénominateurs est nul, il est impossible de résoudre l’équation.
En conclusion, le produit en croix avec des fractions est une méthode simple et efficace pour résoudre des problèmes de proportion. En utilisant cette méthode, on peut facilement trouver la valeur inconnue dans une proportion donnée.
Comment faire un produit en croix pour le théorème de Thalès ?
Le théorème de Thalès est un outil mathématique important pour déterminer les longueurs manquantes dans des figures géométriques. Pour appliquer ce théorème, il est nécessaire de savoir comment faire un produit en croix. Dans le cas du théorème de Thalès, le produit en croix permet de déterminer si deux droites sont parallèles ou non.
Dans la formule CD / AC = CE / BC, les produits en croix sont égaux. Pour les calculer, il suffit de multiplier les termes en diagonale et de les égaliser. Ainsi, on obtient AC x CE = CD x BC. Si l’on connaît trois des quatre valeurs, on peut alors trouver la quatrième.
Dans le cas du théorème de Thalès, on sait que les points A, D et C, ainsi que les points B, E et C, sont alignés dans le même ordre. En utilisant la réciproque du théorème de Thalès, on peut déduire que les droites AB et DE sont parallèles si et seulement si les rapports CD / AC et CE / BC sont égaux.
Pour trouver les valeurs manquantes dans une figure géométrique, il est donc important de maîtriser la technique du produit en croix. Cette formule permet de résoudre de nombreux problèmes en mathématiques, notamment dans le cadre du théorème de Thalès.
Aller plus loin








Leave a Reply